3

Druga zasada dynamiki

 

81.Z jakim przyspieszeniem porusza się ciało m=2kg po poziomej powierzchni pod wpływem poziomej F=20N?  Rozwiązanie YT

 

82.Znajdź przyspieszenie i napięcie nici łączącej m₁=2 kg i m₂=4 kg poruszające się bez tarcia po poziomej powierzchni pod wpływem poziomej F=30 N ciągnącej m₂. Rozwiązanie YT

 

83.Na poziomym stole leży sześć sześcianów o masie m=1 kg każdy. Stała, pozioma siła F=12 N działa na pierwszy z nich. Jaka siła wypadkowa działa na każdy sześcian? Rozwiązanie YT

 

 

84.Linijka o długości d=1 m jest ciągnięta za jeden koniec po poziomym stole przez poziomą siłę F=100 N. Znajdź naprężenie w niej w odległości x=60 cm od jej początku. Rozwiązanie YT

 

85.Znajdź przyspieszenie układu i napięcie nici łączącej masy m₁=3 kg oraz m₂=1 kg. Rozwiązanie YT

 

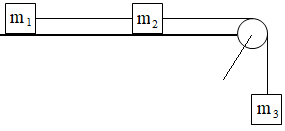
86.Znajdź przyspieszenie układu i napięcia nici łączących masy m₁=2 kg, m₂=4 kg i m₃=1 kg. Rozwiązanie YT

 

 

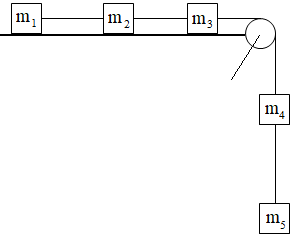
87.Znajdź przyspieszenie układu i napięcia nici łączących masy m₁=1 kg, m₂=2 kg, m₃=3 kg, m₄=4 kg i m₅=5 kg.  Rozwiązanie YT

 

88.Wyprostowany, jednorodny sznur o długości d leży na stole tak, że jego część zwisa. Jak zmienia się jego przyspieszenie w zależności od długości części zwisającej? Rozwiązanie YT

 

89.Z jakim przyspieszeniem porusza się po poziomym stole ciało o m=10 kg pod działaniem F=50 N tworzącej z poziomem a=30^o? Jaką siłą naciska ono na podłoże? Rozwiązanie YT

 

90.Z jakim przyspieszeniem porusza się po poziomym stole ciało m=10 kg pod wpływem poziomej siły F=60 N. Współczynnik tarcia o podłoże m=0,2. Rozwiązanie YT

 

91.Znajdź przyspieszenie mas m₁=1 kg i m₂=2 kg oraz napięcie nici, jeśli F=30 N a m=0,2. Rozwiązanie YT

92.Znajdź przyspieszenie układu i napięcie nici łączących masy m₁=2 kg i m₂=1 kg (patrz rys. do zadania nr 85), gdy współczynnik tarcia masy m₁ o stół jest m=0,2. Rozwiązanie YT

 

93.Znajdź przyspieszenie układu i napięcia nici łączących masy m₁=3 kg, m₂=2 kg i m₃=1 kg, (patrz rysunek do zadania nr 86), gdy współczynnik tarcia mas o stół jest m=0,1. Rozwiązanie YT

 

94.Wyprostowany, jednorodny sznur o długości d leży na stole tak, że jego część zwisa. Jak zmienia się przyspieszenie sznura w zależności od długości jego części zwisającej, jeśli współczynnik tarcia sznura o stół jest m=0,2? (porównaj z zadaniem nr 88). Rozwiązanie YT

 

95.Z jakim przyspieszeniem porusza się po poziomym stole ciało o masie m=10 kg pod działaniem siły F=50N, skierowanej pod kątem a=30^o do poziomu? Współczynnik tarcia ciała o podłoże m=0,2 porównaj z zadaniem

nr 89). Rozwiązanie YT

 

96.Znajdź przyspieszenie mas m₁=1kg i m₂= 2kg oraz napięcie nici je łączącej, która została przerzucona przez nieważki i nieruchomy blok wiszący u sufitu. Rozwiązanie YT

   

97.Znajdź przyspieszenie mas m₁= 2kg, m₂= 3kg, m₃= 4kg oraz napięcia nici je łączących, jeśli nić między masą m₂ i m₃ przerzucono przez blok nieruchomy. Rozwiązanie YT

 

98.Dwie masy M=1 kg każda przyczepiono do końców nitki przerzuconej przez blok nieruchomy. Na jednej z nich położono masę m=0,1 kg. Jakie jest przyspieszenie układu i nacisk masy m na M? Rozwiązanie YT

 

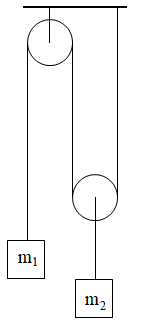
99.Znajdź przyspieszenie mas m₁=4 kg i m₂=5 kg oraz napięcie nici je łączącej, gdy jest ona przerzucona przez dwa nieważkie bloczki: ruchomy i nieruchomy. Rozwiązanie YT

 

100.Sznur o długości d, przerzucony przez poziomy drążek, ślizga się po nim bez tarcia. Jak zmienia się przyspieszenie sznura w zależności od dłuższej części zwisającej x? Rozwiązanie YT

 

101.Jaką siłą, ciało o masie 50 kg, naciska na podłogę windy jadącej z przyspieszeniem: Rozwiązanie YT

1) a = 2,5 m/s² do góry? 

2) a = -2,5 m/s² do góry?   

3) a = 2,5 m/s² w dół?  

4) a = -2,5 m/s² w dół?

 

102.Z jakim przyspieszeniem zsuwa się po równi, o kącie nachylenia a=30^o, ciało o masie m=1 kg? Jaką siłą ciało naciska na równię? Jakie będą przyspieszenie i siła nacisku, gdy pchniemy ciało w górę tej równi?

Rozwiązanie YT

 

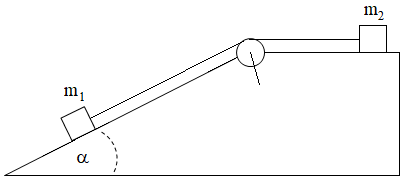
103.Znajdź przyspieszenie mas m₁=1 kg i m₂=2 kg i napięcie nici je łączącej, gdy a=30^o. Rozwiązanie YT

 

 

104.Znajdź przyspieszenie mas m₁=2kg, m₂=4kg i napięcie nici, gdy a=30^o i b=60^o. Rozwiązanie YT

 

 

105.Znajdź przyspieszenie mas m₁=1kg i m₂=2kg, gdy a=30^o. Rozwiązanie YT

 

 

106.Z jakim przyspieszeniem zsuwa się z równi o nachyleniu a=30^o ciało o masie m=1kg? Współczynnik tarcia m=0,2. Rozwiązanie YT

 

107.Z jakim opóźnieniem porusza się ciało o masie m=6kg, pchnięte ku górze równi o nachyleniu a=30^o? Współczynnik tarcia m=0,2. Rozwiązanie YT

 

108.Znajdź przyspieszenie mas m₁=2kg, m₂=4kg i napięcie nici je łączącej, gdy a=30^o i b=60^o jak w

zadaniu 104. Współczynnik tarcia m=0,1. Rozwiązanie YT

 

109.Trzy jednakowe kulki wiszą na trzech jednakowych gumkach, jedna pod drugą. Oblicz przyspieszenie każdej kulki tuż po przecięciu gumki łączącej kulkę górną ze środkową. Rozwiązanie YT

 

110.O jaki kąt od pionu odchyli się lampa wisząca w wagonie poruszającym się z przyspieszeniem a=1m/s² po poziomym torze? Rozwiązanie YT

 

111.Jaki kąt z poziomem utworzy powierzchnia benzyny w cysternie jadącej po poziomym torze z przyspieszeniem a=2,5 m/s²? Rozwiązanie YT

 

112.Jaki jest współczynnik tarcia skrzyni o poziomą platformę ruszającą poziomo z a=4m/s², jeśli nie zmienia ona położenia? Rozwiązanie YT

 

113.Jaką wartość ma siła F pchająca wózek M=5kg, jeśli masy m₁=2kg i m₂=1kg połączone nitką przerzuconą przez blok, są nieruchome względem wózka? Brak tarcia. Rozwiązanie YT

 

114.Na jedną z mas M, przyczepionych do końców nici przerzuconej przez nieruchomy blok, położono m=2g i wtedy ciężarki przebyły s=0,6m w t=3s. Znajdź M. Rozwiązanie YT

 

115.Na końcach nici przerzuconej przez blok nieruchomy wiszą na tym samym poziomie m=0,3kg i M. Po t=2s od ich zwolnienia odległość między nimi była h=4m. Znajdź M. Rozwiązanie YT

 

116.Ciało m=3kg spadło z h=20m. Jak długo zagłębiało się w ziemię, jeśli siła oporu była F=120N? 

Rozwiązanie YT

 

117.Przez nieważki blok nieruchomy wiszący na siłomierzu przerzucono nić, do końców której przymocowano M=10kg i m=3kg. Co wskazał siłomierz? Rozwiązanie YT

118.Gdy ciężar jest podnoszony z a=4m/s² to naciąg liny jest 2 razy mniejszy od jej wytrzymałości. Z jakim największym przyspieszeniem można podnieść ten ciężar za pomocą tej liny? Rozwiązanie YT

 

119.Z jakim największym przyspieszeniem można podnieść ciało m=300kg za pomocą liny o wytrzymałości F=4500N? Rozwiązanie YT

 

120.m=100kg podniesiono za pomocą liny ze stałym przyspieszeniem na wysokość h=80m w czasie t=4s. Jakie było naprężenie liny? Rozwiązanie YT

 

121.Jaką prędkość uzyska spoczywające ciało m=0,4kg pod działaniem poziomej F=10N po przebyciu poziomo s=2m? Rozwiązanie YT

 

122.Parowóz o m=40t jadąc z prędkością v_o=72km/h zaczął hamować i stanął po t=1min 20s. Znajdź siłę hamującą.  Rozwiązanie YT

 

123.Pocisk m=15kg wyleciał z działa z v=850m/s. Jak długo trwał lot przez lufę, jeśli średnia siła działająca na pocisk była F= 3∙ 10⁶N? Rozwiązanie YT

 

124.Połączone nitką m₁=100g i m₂=200g leżą na poziomej powierzchni. Jaką maksymalną, poziomą siłą można ciągnąć pierwsze ciało, jeśli wytrzymałość nici jest F=10N? Jaką maksymalną poziomą siłą można ciągnąć drugie ciało? Rozwiązanie YT

 

125.Pociąg hamując na poziomym torze, zmienia jednostajnie swoją prędkość od v₁=36km/h do v₂=18km/h w czasie t=5s. O jaki kąt odchyli się od pionu wahadło wiszące w jednym z przedziałów? Rozwiązanie YT

 

126.Jaki jest kąt nachylenia deski, jeśli przyspieszenie zsuwającego się z niej ciała jest dwa razy mniejsze od przyspieszenia ziemskiego? Brak jest tarcia. Rozwiązanie YT

 

127.Jakie nachylenie winien posiadać dach domu, aby krople ściekały po nim w najkrótszym czasie? 

Rozwiązanie YT

 

128.Wysokość równi o kącie nachylenia a=30^o jest h=5m. Jak długo zsuwa się z niej ciało bez tarcia? 

Rozwiązanie YT

 

129.W ciągu t=1,5s ciało przybyło bez tarcia długość s=1,5m równi pochyłej i potem taką samą drogę na poziomej powierzchni. Jaki jest kąt nachylenia równi? Rozwiązanie YT

 

130.Jaki był kąt nachylenia równi, jeśli klocek położony na niej przebył bez tarcia s=2,4m w ciągu t=2s?  Rozwiązanie YT

 

131.Jaki był kąt nachylenia równi, jeśli klocek na niej położony w ciągu szóstej sekundy przebył 24m?  Rozwiązanie YT

 

132.Ze szczytu równi o długości s=2m i nachyleniu a=30^o ruszyło ciało A, a od podstawy równi ciało B. Jaką prędkość nadano ciału B, jeśli spotkały się one w połowie drogi? Rozwiązanie YT

 

133.Z najwyższego punktu równi o nachyleniu a=45^o zaczyna się zsuwać bez tarcia ciało A. W tej samej chwili, z tej samej wysokości, zaczyna swobodnie spadać ciało B. Jaką część równi przebędzie A do chwili upadku na równię B? Rozwiązanie YT

 

134.Jaką prędkość należy nadać ciału pchniętemu ku górze równi o wysokości h=2m i nachyleniu a=30^o, aby osiągnęło szczyt po t=1s? Jaką wtedy miało prędkość? Rozwiązanie YT

 

135.Jaką prędkość początkową należy nadać ciału pchniętemu ku górze równi pochyłej o wysokości h=1m i nachyleniu a=30^o, aby szczyt osiągnęło z  prędkością v=0? Rozwiązanie YT

 

136.Z równi o nachyleniu a=30^o ciało ześlizguje się bez tarcia t₁=15s a z tarciem t₂=20s. Jaki jest współczynnik tarcia? Rozwiązanie YT

 

137.Samochód o m=1500kg wjeżdża ze stałą prędkością na zbocze o nachyleniu h=1m na każde s=25m drogi. Siła oporu jest równa k=0,08 jego ciężaru. Znajdź siłę ciągu silnika. Rozwiązanie YT

 

138.Z jakim przyspieszeniem porusza się poziomo równia o nachyleniu a=30^o, jeśli klocek m=1kg pozostaje na niej w tym samym miejscu? Znajdź nacisk klocka na równię. Rozwiązanie YT

 

139.Masy m₁=4kg i m₂=6kg w chwili początkowej spoczywają na tej samej wysokości. Jaka odległość dzieli je po t=2s od chwili ich puszczenia? Rozwiązanie YT

140.Pod wpływem tarcia, na poziomej drodze s=100m samochód zmniejszył prędkość z v_o=15m/s do v=10m/s. Znajdź współczynnik tarcia. Rozwiązanie YT

 

141.Pocisk m=10g, lecąc poziomo z v_o=300m/s, uderzył w deskę o grubości d=4cm i wyleciał z niej z v=100m/s. Jaki był opór deski? Rozwiązanie YT

 

142.Z jaką prędkością masa m₁=1kg uderzy w podłogę, jeśli w chwili początkowej znajdowała się na wysokości h=1m, a układ spoczywał? Współczynnik tarcia masy m₂=4kg jest m=0,025. Rozwiązanie YT

 

143.Układ m₁=1kg i m₂=2kg w chwili początkowej spoczywał. Jaką drogę wzdłuż równi przebyła m₁ od chwili uderzenia m₂ w podłoże? a=30^o, h=4m. Rozwiązanie YT

 

144.Po jakim czasie pojazd m=100kg jadący poziomo z v_o=72km/h zatrzymał się pod wpływem sił tarcia F=500N?  Rozwiązanie YT

 

145.Na spoczywający na poziomej powierzchni klocek m=20kg zaczęła działać pozioma siła F=12N. Jaką prędkość miał on po t=5s? Rozwiązanie YT

 

146.Pod wpływem siły F=150N ciało zmieniło swoją prędkość o Dv=6m/s w ciągu t=20s. Jaka była jego masa?Rozwiązanie YT

 

147.Do spoczywającego na stole klocka o m=10kg przyłożono poziomo dwie równe siły F. Jakie przyspieszenie on uzyskał, jeśli F=5N i a=60^o. Rozwiązanie YT

148.Dwa klocki jednocześnie ruszają wzdłuż równi o nachyleniach a=30^o i b=60^o, których wysokości różne, a podstawy s. Które ciało szybciej osiągnie podstawę równi? Rozwiązanie YT

149.Dwa klocki jednocześnie ruszają wzdłuż równi o nachyleniach a=30^o i b=60^o, których wysokości są h a podstawy różne. Które ciało szybciej osiągnie podstawę równi? Rozwiązanie YT

150.Wieżowiec, który powstał w miejscu zniszczonych biurowców WTC w wyniku zamachu z 11 września 2001r. ma wysokość541m. Rusza w nim w górę z przyspieszeniem winda, w której na wadze stoi człowiek o m=60kg. Winda przebyła s=144m w t=6s. Co wskazywała waga? Rozwiązanie YT

 

151.W jednym z wysokich budynków na Manhattanie rusza w dół z przyspieszeniem winda, w której człowiek m=60kg stoi na wadze. Winda przebyła s=144m w t=6s. Co wskazywała waga? Rozwiązanie YT

 

152.Jakie jest napięcie liny, po której małpa o masie m=50kg wspina się z przyspieszeniem a=0,5m/s² względem podłogi?  Rozwiązanie YT 

 

153.Tramwaj porusza się poziomo z a=5m/s². O ile od pionu odchyla się człowiek, aby się nie przewrócić?  Rozwiązanie YT

 

154.Jakie jest przyspieszenie samolotu na pasie startowym, jeśli zawieszone w nim wahadło odchyliło się od pionu o a=45^o? Rozwiązanie YT

 

155.Wykres przedstawia zależność prędkości od czasu ciała o m=8kg. Jakie siły działały na nie w drugiej i piątej sekundzie?  Rozwiązanie YT

 

156.Wykres przedstawia zależność od czasu siły, która zaczęła działać na ciało m=10kg poruszające się ze stałą prędkością v_o=4m/s. Jaką prędkość posiada ono  po t=3s działania siły F? Rozwiązanie YT

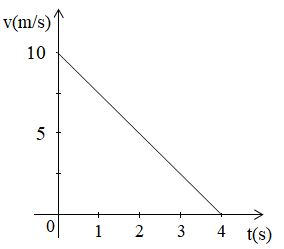
157.Wykres przedstawia zależność prędkości od czasu klocka po poziomej powierzchni. Jaki jest współczynnik tarcia? Rozwiązanie YT

 

 

 

 

 

 

D3.1. Kulkę o masie m zawieszono na nici tworzącej z sufitem w stanie równowagi kąty a i b. Znajdź naprężenia nici. YT

 

D3.2. Znajdź przyspieszenie po poziomym stole równi o nachyleniu a=30o, przy którym klocek o m=5kg pozostaje w tym samym miejscu równi. Nie ma tarcia między ciałem i równią a podłożem. Jaki jest wtedy nacisk ciała na równię? Porównaj z naciskiem, jaki wywierałoby ciało na nieruchomą równię. Przyjmij g=10m/s2. YT

 

 

 

 

D3.5. Do walca o m=5kg i r=50cm leżącego na przedostatnim stopniu schodów o h=25cm, przyłożono poziomą F. Przy jakiej jej wartości walec pokona stopień? Przyjmujemy g=9,81m/s². YT

 

D3.6. Z wysokości h=5m równi pochyłej o masie M=10kg zsuwa się klocek o masie m=1kg. Znajdź prędkości obu ciał po zsunięciu się klocka. Brak jest tarcia. Przyjmij g=10m/s². YT

 

D3.7.

 

D3.8. W windzie, która może poruszać się w górę i w dół z przyspieszeniem o takiej samej wartości, na wadze sprężynowej   stoi dziewczyna. Różnica wskazań wagi przy ruchu w górę i w dół wynosi 50N. Jakie jest przyspieszenie windy,   jeżeli ciężar dziewczyny jest 500N? YT

 

D3.9.Szklane naczynie w kształcie sześcianu o bokach a=40cm napełniono do wysokości h=30cm wodą i ustawiono w wagonie kolejowym tak, że jedna z jego krawędzi była równoległa do kierunku jazdy. Znajdź przyspieszenie pociągu, przy którym woda zaczęła wylewać się z naczynia. Przyjmij g=9,8m/s². YT

 

D3.T.1. Jak przedstawiać siły? YT

 

D3.T.2. Siły tarcia działające na ciało na poziomej nieruchomej powierzchni. YT

 

D3.T1. Jaką poziomą siłę należy przyłożyć do spoczywającego na poziomej powierzchni  klocka o m=1kg, aby on ruszył? Współczynnik tarcia m=0,2. Przyjmij g=9,81m/s². YT

 

D3.T2. Do  spoczywającego na poziomej równi klocka o m=5kg przyłożono poziomą F=15N. Znajdź jego przyspieszenie, gdy m=0,2. Przyjmij g=10m/s².  YT

 

D3.T3. Klocek o m=1kg pchnięto po poziomej równi. Znajdź jego przyspieszenie, gdy m=0,2. Przyjmij g=10m/s².  YT

 

D3.T4. Do pchniętego po poziomej powierzchni klocka o m=1kg przyłożono poziomą, przeciwną do prędkości F=5N. Znajdź jego przyspieszenie, gdy m=0,1. Przyjmij g=10m/s².  YT

 

D3.T5. Klocek o masie m=2kg leży na poziomym stole ustawionym w windzie drapacza chmur.  Jakie przyspieszenie nada klockowi pozioma F=10N, gdy winda porusza się z a_w=5m/s² do góry a m=0,2. Przyjmij g=10m/s². YT

 

D3.T6. Klocek o masie m=2kg leży na poziomym stole ustawionym w windzie wysokiego drapacza chmur.  Jakie przyspieszenie nada klockowi pozioma F=10N, gdy winda porusza się z a_w=5m/s² w dół a m=0,2. Przyjmij g=10m/s². YT

 

D3.T7. Jakie jest przyspieszenie klocka o m=2kg, zsuwającego się bez tarcia z równi o nachyleniu a=30^o? Jaka jest siła nacisku na równię? Przyjmij g=10m/s². YT

 

D3.T8. Siła tarcia na równi pochyłej podczas ruchu ciała w jej dół. YT

 

D3.T9. Jakie jest poziome przyspieszenie równi o nachyleniu a=30^o, przy którym klocek na niej pozostaje w tym samym jej miejscu? Brak jest tarcia. Przyjmij g=10m/s².  YT

 

D3.T10. Z jakim przyspieszeniem zsuwa się klocek wzdłuż równi o nachyleniu a=30^o znajdującej się w windzie poruszającej się z a_w=2,5m/s² w dół? Brak jest tarcia. Przyjmij g=10m/s². YT

 

D3.T11. Z jakim przyspieszeniem zsuwa się klocek wzdłuż równi o nachyleniu a=30^o znajdującej się w windzie poruszającej się z a_w=2,5m/s² do góry? Brak jest tarcia. Przyjmij g=10m/s². YT

 

D3.T12. Z  jakim przyspieszeniem zsuwa się z nieruchomej równi o nachyleniu a=60^o klocek, gdy m=0,2 i g=10m/s²? YT

 

D3.T13. Z  jakim przyspieszeniem porusza się w górę równi o nachyleniu a=60^o klocek, gdy m=0,2 i g=10m/s²? YT

 

D3.T14. Znajdź przyspieszenie po poziomym stole równi  o nachyleniu a=15^o, przy którym klocek o m=5kg rusza w dół równi. Jest  tarcie i m=0,5. Jaki jest nacisk ciała na równię? Porównaj go z naciskiem, jaki wywierałby klocek na nieruchomą równię. Przyjmij g=10m/s². YT

 

D3.T15. Znajdź przyspieszenie po poziomym stole równi  o nachyleniu a=15^o, przy którym klocek o m=5kg rusza w górę równi. Jest  tarcie i m=0,5. Jaki jest nacisk ciała na równię? Porównaj go z naciskiem, jaki wywierałby klocek na nieruchomą równię. Przyjmij g=10m/s². YT

 

D3.T16. Dwa klocki o masach m₁=1kg i m₂=2kg połączone nierozciągliwą nitką są ciągnięte siłą F=8N o nachyleniu α=30^o.  Współczynniki tarcia klocków o poziomy stół  są m₁=0,1 i m₂=0,2. Znajdź przyspieszenie układu i napięcie nici. YT

 

 

 

D3.10. Znajdź przyspieszenie układu wiedząc, że

bloki nieruchome mają m=0,5kg i r=0,1m

oraz m₁=1kg, m₂=2kg, m₃=3kg. Nici nie ślizgają się

po blokach, a m₂ ślizga się po stole bez tarcia. YT

 

 

 

 

 

 

D3.T16a. Skrzynia o m=50kg znajduje się w naczepie samochodu ciężarowego. Współczynniki tarcia skrzyni o podłogę są: statycznego m_s=0,4 i kinetycznego m_k=0,3. Skrzynia będzie spoczywać względem podłogi czy też po niej się ślizgać, gdy samochód  poruszał się będzie z przyspieszeniem raz a₁= 2m/s² a drugi raz a₂= 5m/s²? YT

 

 

D3.10.a. Klocki o  m=2kg i M=4kg połączono nicią, która może się ślizgać bez tarcia po unieruchomionym na ścianie bloczku. Znajdź wartość siły F, dzięki której klocki poruszają się jednostajnie, jeśli współczynnik tarcia kinetycznego między wszystkimi powierzchniami jest m=0,4. YT

 

 

D3.11. Koniec drabiny o m_d=20kg, długości l=20m i środku masy w odległości l₁=l/3 od podłoża oparty jest o pionową, gładką ścianę na wysokości h=16m. Człowiek o m_c=60kg znajduje się na niej w odległości l₂=l/2. Znajdź wartość sił działających na drabinę przez ścianę i podłoże pamiętając, że poziome podłoże nie jest gładkie. YT

 

D3.12. Z parteru wieży telewizyjnej ruszyła z przyspieszeniem a winda. Po uzyskaniu v=7m/s jednostajnie przebyła drugą część drogi. Trzecią część przebyła z opóźnieniem a osiągając po t=60s szczyt na wysokości H=322m. Znajdź a. YT

 

D3.12.a. Na poziomym stole znajdują się dwie identyczne równie pochyłe, o takich samych masach. Jedna jest przymocowana do stołu (1), a druga swobodna (2). Klocek o masie 100g rozpędzano po stole nadając mu prędkość 4m/s skierowaną ku jednej, a potem ku drugiej równi pochyłej. Na równi (1) klocek wzniósł się na wysokość H. Równia (2) ruszyła, a klocek wzniósł się na wysokość h w chwili, gdy jej prędkość osiągnęła wartość 0,5m/s. Tarcie nie występuje. Znajdź stosunek H/h. YT