...który wziął prysznic

Miałem gościa...

2.2.Wzory na drogę w ruchu jednostajnie zmiennym

          Pole pod wykresem zależności prędkości od czasu liczbowo jest równe przebytej drodze. Dla ruchu jednostajnie zmiennego pole to jest trapezem o bokach v i v_o oraz wysokości t.(patrz poniższy rys.).

          Zatem przebyta w tym ruchu droga jest 

.

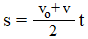
          Zwróćmy uwagę na to, że ułamek w powyższym wzorze to prędkość średnia w ruchu jednostajnie zmiennym (średnia arytmetyczna v_o i v). 

            Gdy podstawimy wzór v=v_o+at to po uproszczeniach mamy

.

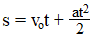
          Za pomocą tego wzoru możemy liczyć też drogę przebytą w ruchu jednostajnie opóźnionym. Wtedy wartość przyspieszenia winniśmy brać ze znakiem minus.

          Dla ruchu bez prędkości początkowej jest

.

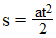
        Rozwiązując zadania z kinematyki ruchu jednostajnie zmiennego będziemy korzystać z tych wzorów.

         Z przedstawionych wzorów wynika, że w ruchu jednostajnie zmiennym droga zależy wprost proporcjonalnie od kwadratu czasu. Wykresem takiej zależności są parabole.